DSA - 2 Linked Lists

Arrays with nodes

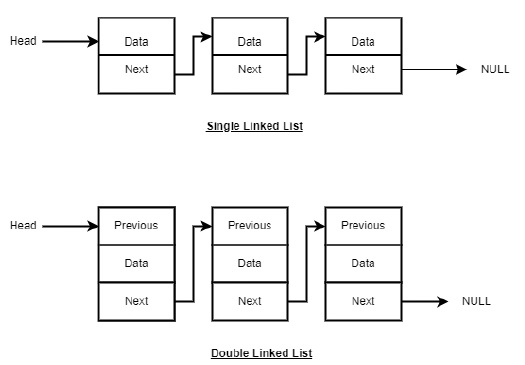
A linked list stores data fundamentally different from an array. Instead of a collection sitting side by side in memory. A linked list is a single object floating in heap space. It contains some data units, and a reference to the next item (memory address).

We have 2 types of linked lists, single and double. Single linked lists stores a references to the next node in the list, but not the previous. Double linked lists stores a reference to the next and the previous node.

---

Linked list specs

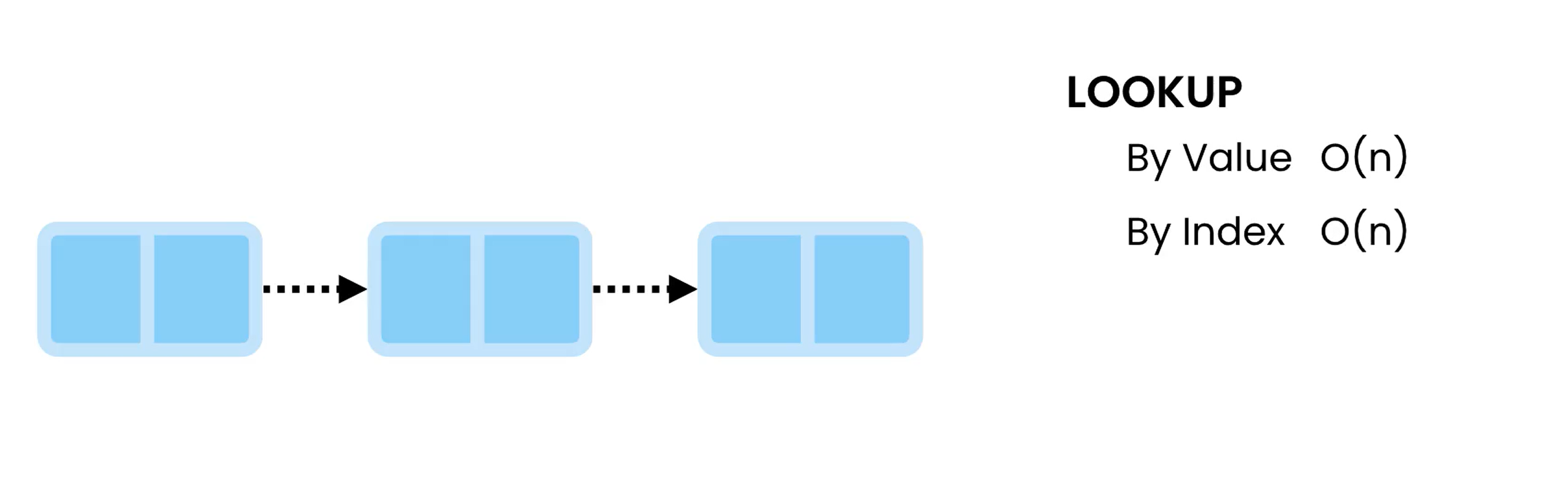
Lookup

Lookups in linked lists are always O(n) complexity as we can only do sequencial searches. Since every item is stored non continously in memory, we have to traverse the list to find by value, and by index.

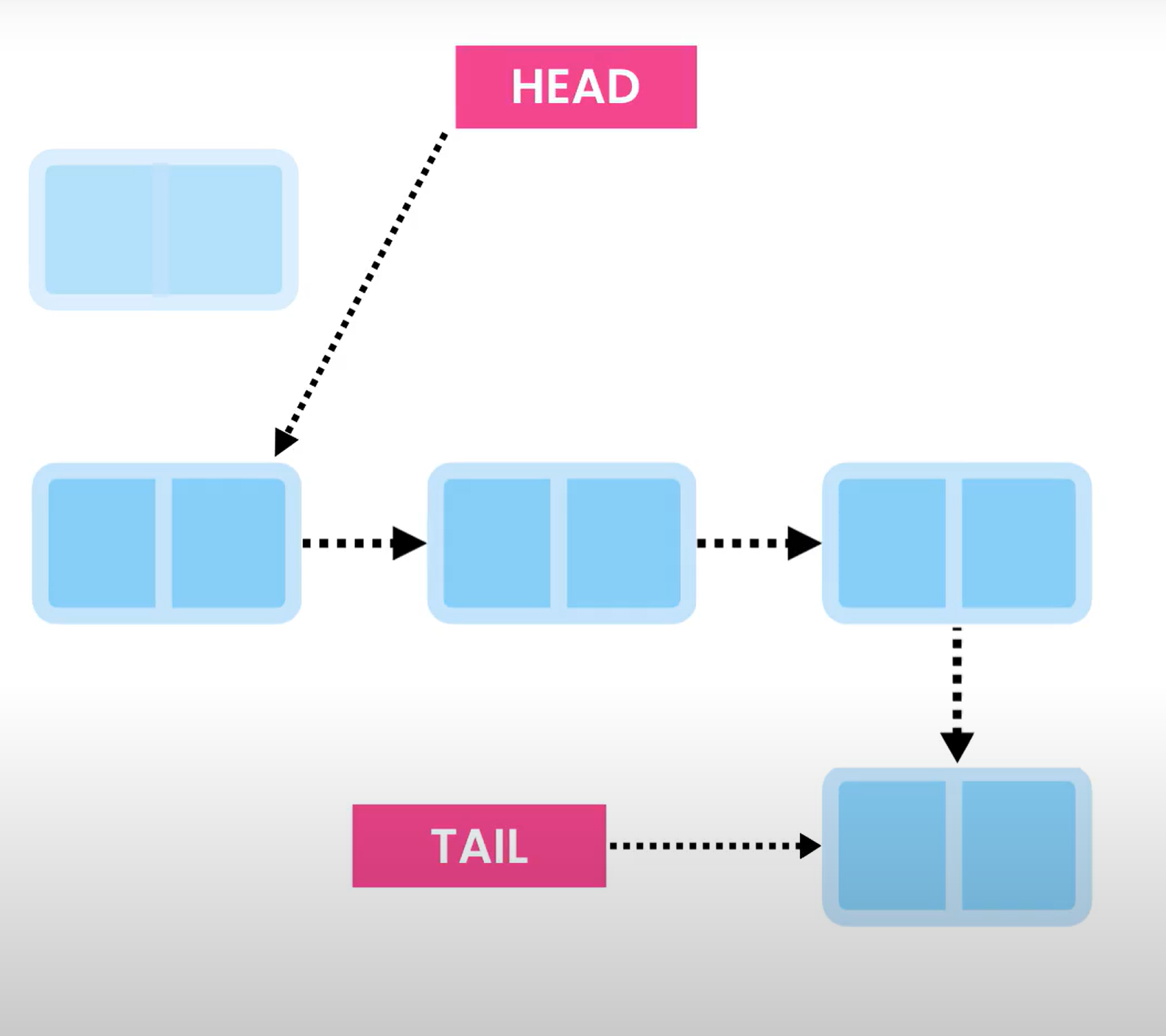
Insertion

Insertions depends on where it is done. Insertions on the head or tail is a O(1) complexity, as we can always store a reference to the head or tail, however, the same cant be said for items in the middle

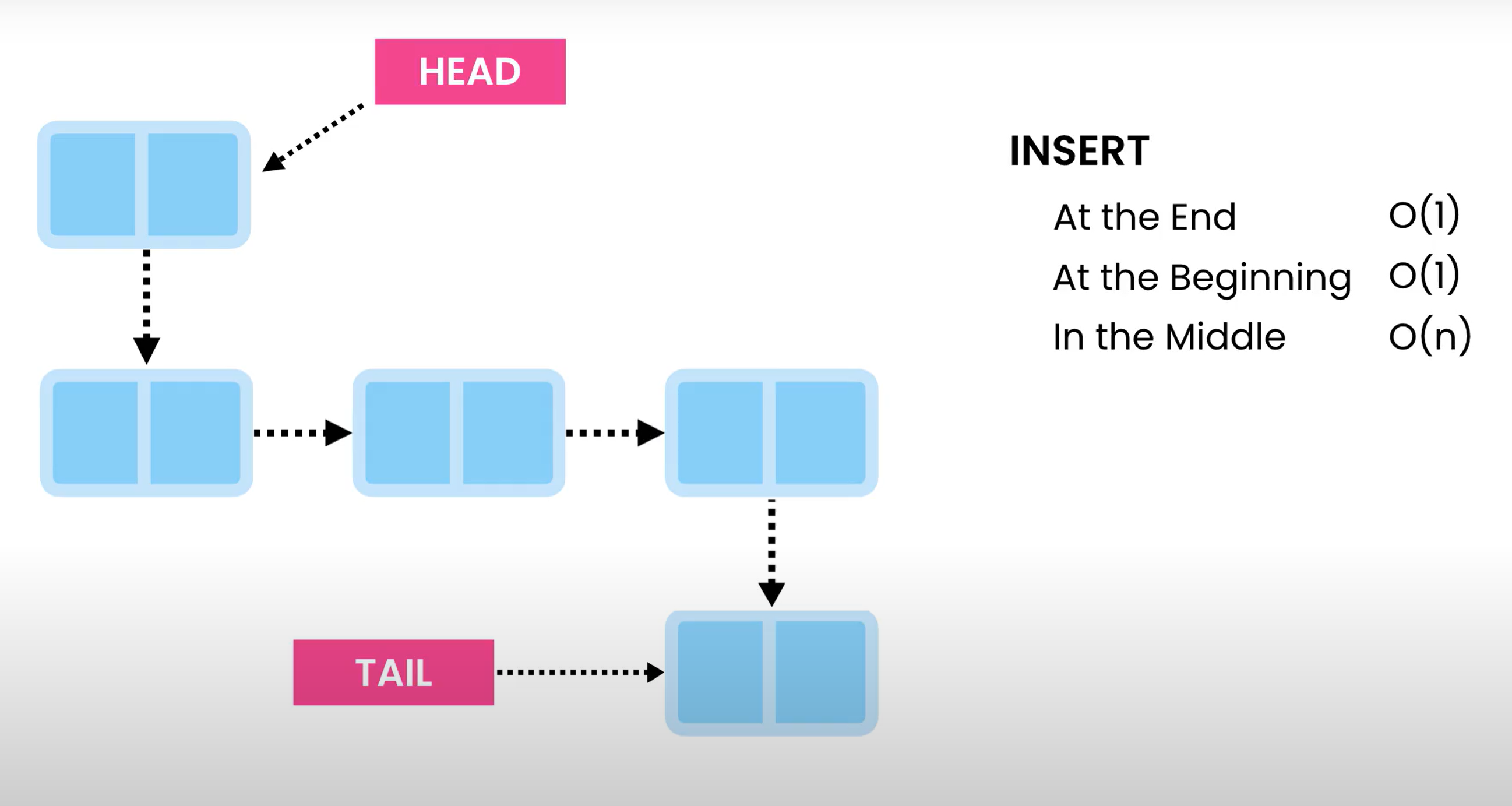When we add an item to the head of the list. We create a node that contains the data, we assign its pointer to the original first item. then store this new node as the head.

For the tail, we create a new note, and have the last note point to it, and assign the new node as the tail.

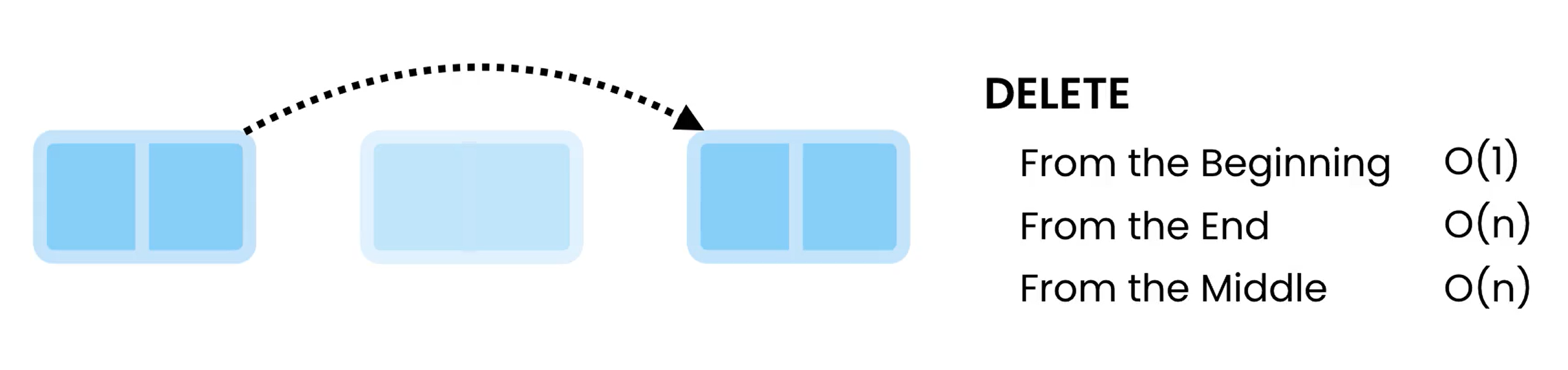
Deletion

Deletion for the head is super fast, and is a O(1) operation as we simply need to point the head to the second item in the list and remove the first item’s reference.

However, in single linked lists, deleting the last item is a O(n) as we do not have a reference pointing to the second last item, so we need to traverse it.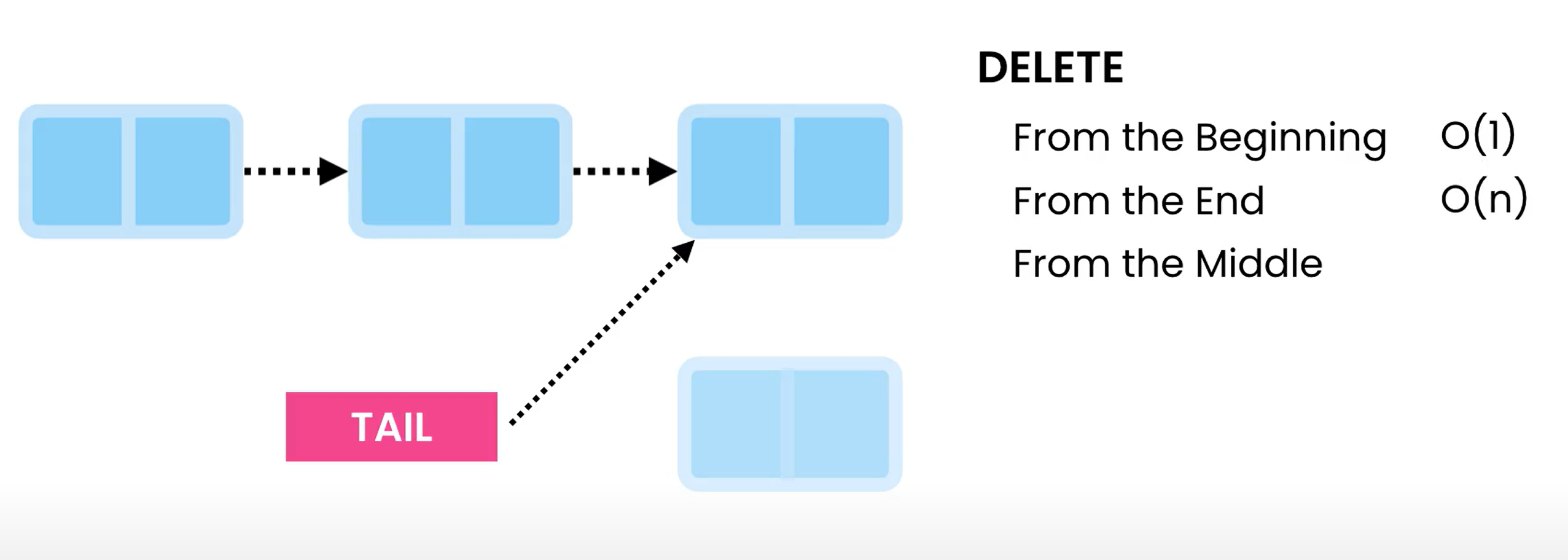

For somewhere in the middle, we have to unlink the previous item reference and have it skip the deleted node to point to the next node. Since we have to traverse the node it is an O(n) operation.

---

Implementation: Singular linked lists

A linked list class consists of 2 fundamental structures: an internal Node class and the linked lists class:

public class LinkedLists {
    private Node head;
    private Node tail;
...
}

internal class Node {
    public int data;
    public Node? next;
    public Node(int data, Node? next) {
        this.data = data;
        this.next = next;
    }
}

Adding items at begining and end of list

Adding items at the begining and the end of the list is very simple. All we needed to do was to create a new node object to hold a value, and swap the references around.

public void addLast(int value) {
    var node = new Node(value, null);
    if (head == null) 
        head = node;
    else 
        tail.next = node;
    tail = node;
}
public void addFirst(int value) {
    var node = new Node(value, null);
    if (head == null)
        tail = node;
    else 
        node.next = head;
    head = node;
}

Small improvements
We can also improve the if list is empty check by declaring this method:\

private bool isEmpty() {
    return (head == null);
}

This way we can do if (isEmpty()) {..} instead of if (head == null) {..}

Index of - search

There are 2 ways we can do an index of search:

1. Recursively traverse the array and return the index once found
2. While loop

Recursive solution

You need an index counter, and starting with the first node. Base collapse cases are found and when hit the last node.

public int indexOf(int value) {
    return find(head, value);
}

private int index = 0;
private int find(Node node, int? item)  {
    
    if (node.data == item)
        return index;
    if (node.next == null)
        return -1;
    index++;
    return find(node.next, item);
}

While loop solution

We define the same breaking case: if found return index; else continue. If currentNode == null, breaks out of the while loop, and return -1.

public int indexOf(int value){
    var index = 0;
    var currentNode = head;
    while (currentNode != null) {
        if (currentNode.data == value)
            return index;
        index++;
        currentNode = currentNode.next;
    }
    return -1;
}

contains

This is relatively simple as we can use the indexOf method to iterate through the list and check for -1 returns.

public bool contains(int value) {
    return (indexOf(value) != -1);
}

Removing first and last item

Removing the first item is fairly straight forward. Remove the reference to the second item from the first, then add the second item as a head. Removing the last item would require traversing the list to get to the second-last item. Set its reference to null, then set it as the new tail.

public void removeFirst() {
    if (isEmpty())
        throw new InvalidOperationException(
            "cannot remove item from empty list"
        );
    if (head == tail)
        tail = null;
    
    var oldHead = head;
    head = oldHead.next;
    oldHead.next = null;
}

public void removeLast() {
    if (head == null)
        throw new InvalidOperationException("Cannot remove item from empty list");
    
    if (head == tail) {
        head = null;
        tail = null;
        return;
    }
    var currentNode = head;
    while (tail != currentNode.next) {
        currentNode = currentNode.next;
    }
    
    currentNode.next = null;
    tail = currentNode;
}

Convertion to array

There are a few ways to convert a linked list into an array. Apending them to a list, convert and return it.

private List<int> items = new List<int>();
public int[] toArray() {
    items.Clear();
    iterate(head);
    return items.ToArray();
}
private void iterate(Node node) {
    if (node.next == null) {
        items.Add(node.data);
        return;
    }
    iterate(node.next);
}

More efficiently, utilizing the size of property and allocate an array, populate and return it.

public int[] toArray() {
    var array = new int[size];
    
    var currentNode = head;
    var index = 0;
    while (currentNode != null) {
        array[index] = currentNode.data; 
        index++;
        currentNode = currentNode.next;
    }
    return array;
}

---

Dynamic Arrays vs Linked lists

Arrays have a fixed sizes, while dynamic arrays grow by 50-100% once they hit a capacity, which leads to unnecessary memory usage.

Linked lists dont waste memory however they do have a slight overhead, because each node stores an address to the next node and a data.

Use arrays if you know the number of items to store.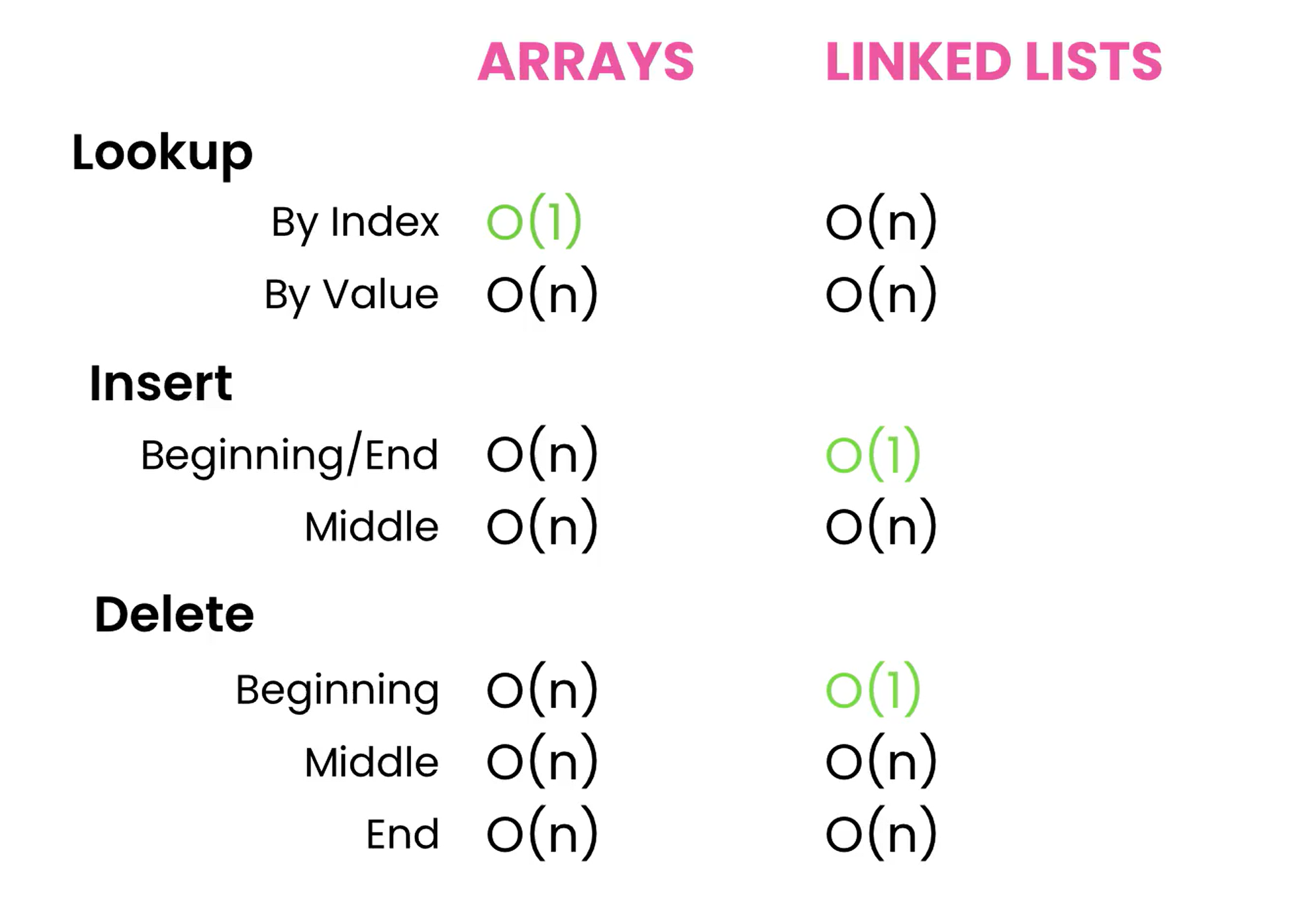

---

Double linked lists

Double linked lists has increased performance for deleting items from the end of the list, as it now stores a reference to the previous node. However the performance comes at a cost of overhead, as we are allocating a new field to track the previous node.

---

References

https://www.tutorialspoint.com/data_structures_algorithms/linked_list_algorithms.htm

https://www.simplilearn.com/tutorials/data-structure-tutorial/linked-list-in-data-structure#:~:text=View%20More,reference%20to%20the%20next%20node.

https://www.geeksforgeeks.org/data-structures/linked-list/