DSA - 1 Arrays and Memory Locality
The most primitive data structure.
After learning at least one programming language, you have definitely came accross arrays. The array is always statically typed and sized.
An array store your data one after another on a single line row of memory location. And since each of the element in your array is predefined and fixed.
1
2
// a byte array
byte[] myArray = new byte[8];
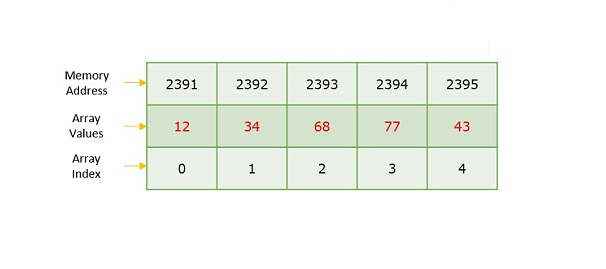
The computer can optimally access the location of your data via an index, since all they needed to do is to jump the memory address using simple + or - operators. This is possible as arrays are contiguous.
Each memory address corresponds to a single byte (8bits).
Time complexity of accessing an array item via index?
Lookup =O(1)
Arrays can just access an item in an index by just calculating the memory location of the item based on the size of each item and the given index
Why are they fast?
Arrays are fast due to the nature of how they are stored in your memory (ram). We know arrays are zero indexed, and statically typed, and that their addresses are contiguous.
Contiguous memory is important. For example. say I allocate memory for a single float 32. This allocates 4 bytes of memory and these 4 bytes are continuous one after another without any gaps in between.
1
2
1 2 3 4
... ... ...[] [] [] [] .... .... ...
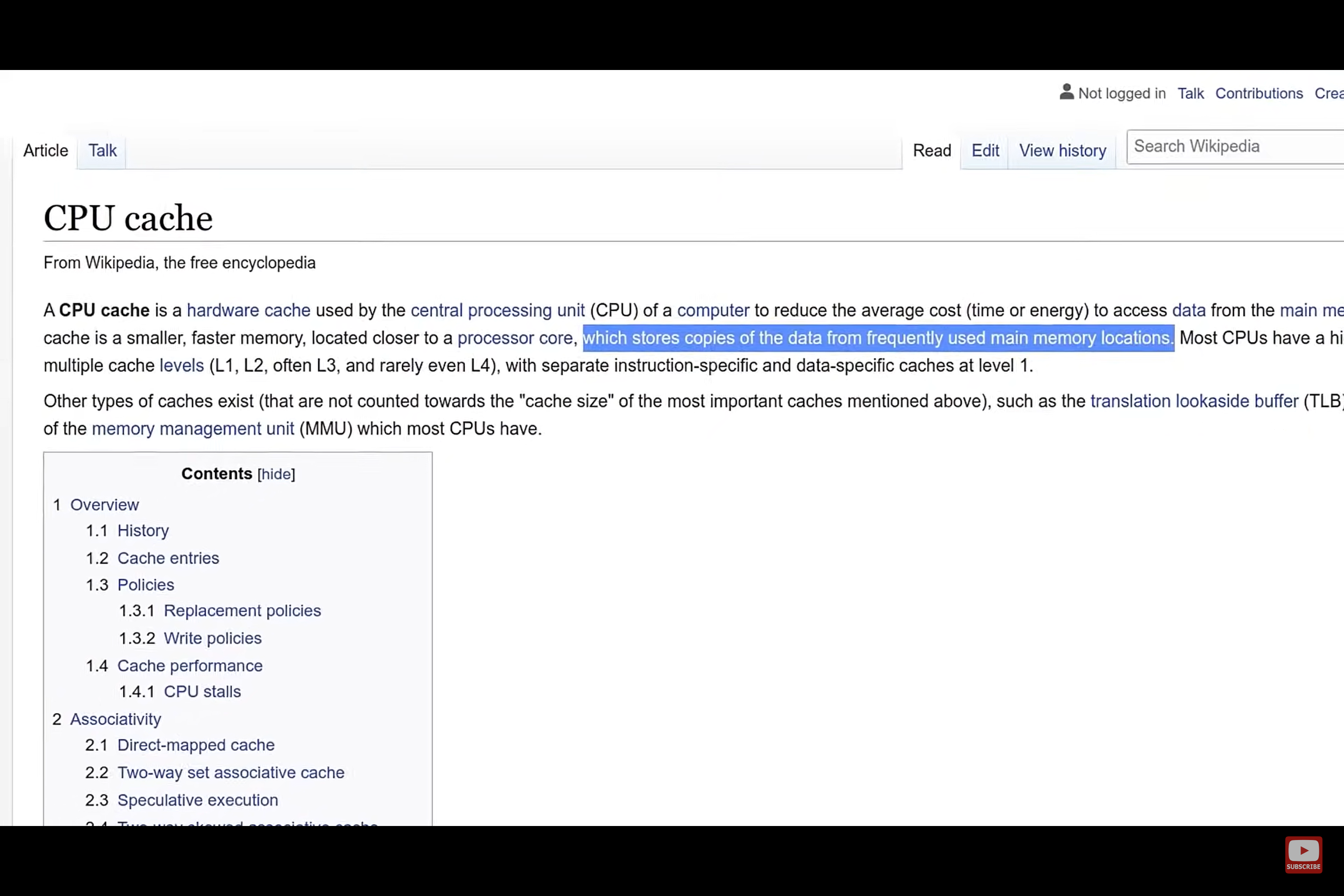
With continous memory, the CPU does not need to fetch new data from the RAM, instead, CPU could hold these data in their cache, reducing cache misses.
This is what L1, L2, and L3 cache on your CPU is for:
Cache Hits Cache miss?
When CPU wants to access data for processing, they do not always find it from the RAM first, and they dont request a single byte.
Instead they would first check the L1 cache, if they found, its a hit, else then the L2, then L3 and finally if it is not in any of the cache. They will request the RAM for the data, usually in a batch of, 64bits for x64 CPUs. This is called a cache line.
This is important, as each subsequent levels are larger in capacity, yet also larger in latency. This is why ensuring contiguous memory in ram is important as we want to minimize as little cache misses and we can.
Non-contiguous memory would result in gaps within our arrays where the CPU will have to refetch from RAM for the subsequent data. This happens often with more complicated data structure such as Linked-lists, and arrayLists.
Array Limitations
Arrays are fast when we perform contiguous operations and calculations. However when it comes to things like query or searches, insertion and deletion. Arrays would suffer some penalty.
Insertion is slow
Since arrays are fixed sized, adding a 6th item to a 5 item sized array would require declaring a new array, copying all the items from the old array.
Removing is slow
Removing an item from the end of an array is pretty easy. We can look up the last item by its index and clear them.
1
2
// Best case Delete o(1)
[1][5][1][6] --> [1][5][1][ ]
However the same cant be said on the first item or at other indexes. Deletion and inserting items into an array at a specific index would require copying and shifting all the items after the target index. this is computationally expensive.
1
2
3
// worse case Delete O(n)
[1][5][1][6] --> [ ][5][1][6] --> shifting [5][1][6][]
^ <------
Item search is slow
When we want to search if an array contains an item. We have to iterate thru the entire array to look for the item. This tedious brute force method may out weights cache benefits when the array is very large.
This is why complex data structures like dictionaries and trees exist.
Practical: Build a dynamically sized Array
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
public class DynamicIntArray {
private int[] array;
private int lastInsertedIndex;
public DynamicIntArray(int arraySize) {
array = new int[arraySize];
lastInsertedIndex = 0;
}
public int getItem(int index) {
if (array.Length - 1 > index) {
return array[index];
}
return 0;
}
public void insert(int item) {
if (array.Length - 1 < lastInsertedIndex) {
int[] temp = new int[array.Length * 2];
Array.Copy(array, temp, array.Length);
array = temp;
}
array[lastInsertedIndex] = item;
lastInsertedIndex++;
}
public void removeAt(int index) {
if (lastInsertedIndex < index || index < 0)
throw new IndexOutOfRangeException("Negative and out of range indexes are not accepted");
lastInsertedIndex--;
for (int i = index; i < lastInsertedIndex; i++) {
array[i] = array[i + 1];
}
int[] temp = new int[lastInsertedIndex];
Array.Copy(array, temp, lastInsertedIndex);
array = temp;
}
public int indexOf(int item) {
for (int i = 0; i <= lastInsertedIndex; i++) {
if (array[i] == item)
return i;
}
return -1;
}
public void print() {
Console.WriteLine($"[{String.Join(", ", array)}]");
}
}
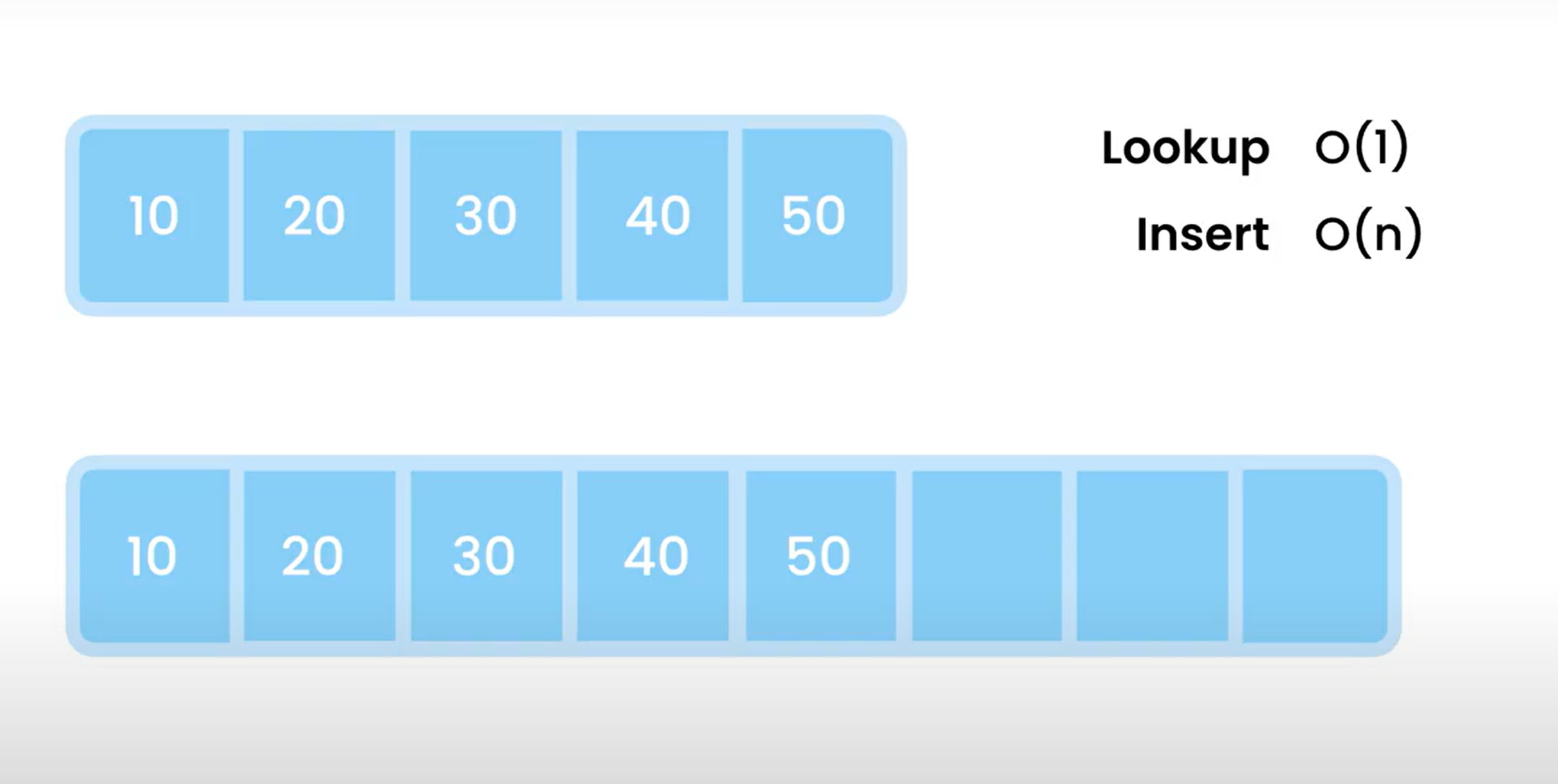
Dynamically sized arrays
Dynamically sized arrays are just like arrays, but they can expand and have no size constrains
An example of a dynamically sized array is the List in C#. Or just list in python.
There are also other examples of dynamic arrays such as ArrayLists. However, there are a clear and distinct difference in their low level representation:
Lists are generic
They are predefined with a type and holds a constrains. This means internally they are an array where each item is lined up one after another in memory address.
List are about as fast as they typically declared and allocates more memory than you need, allowing some contiguous memory. Under the hood, they are just regular arrays with a bit more mechanism. However one key difference is that they are much faster when it comes to adding and removing elements.
When it comes to indexing and accessing individual elements, arrays are definitely always faster.
ArrayLists are non-generic
They do not have a fixed type, value types stored via boxing into a base level object, and stored in the heap. Boxing and unboxing is computationally expensive, therefore it is generally best avoided to use non-generic.
A simple analogy of how it works in the low level. Take an int, and convert it into a type base class object which is the base class of all data types. This object is chucked in the heap. Store its memory address in your Array List. Calling and making sense of this item would require casting it back into desired object. [[Boxing and Unboxing|Readmore]]
Cache Locality in Multidimensional arrays
from an answer on Stack overflow
Just generally speaking, the most efficient loops through a matrix are going to cycle through the last dimension, not the first (“last” being c in m[a][b][c]).
For example, given a 2D matrix like an image which has its pixels represented in memory from top-left to bottom-right, the quickest way to sequentially iterate through it is going to be horizontally across each scanline, like so:
1
2
3
4
for (int y=0; y < h; ++y) {
for (int x=0; x < w; ++x)
// access pixel[y][x]
}
… not like this:
1
2
3
4
for (int x=0; x < w; ++x) {
for (int y=0; y < h; ++y)
// access pixel[y][x]
}
… due to spatial locality. It’s because the computer grabs memory from slower, bigger regions of the hierarchy and moves it to faster, small regions in large, aligned chunks (ex: 64 byte cache lines, 4 kilobyte pages, and down to a little teeny 64-bit general-purpose register, e.g.). The first example accesses all the data from such a contiguous chunk immediately and prior to eviction.
harold on this site gave me a nice view on how to look at and explain this subject by suggesting not to focus so much on cache misses, but instead focusing on striving to use all the data in a cache prior to eviction. The second example fails to do that for all but the most trivially-small images by iterating through the image vertically with a large, scanline-sized stride rather than horizontally with a small, pixel-sized one.
Also, when we increase block size, but keep cache size and associativity constant, does it influence the miss rate? At a certain point increasing block size can cause a higher miss rate, right?
The answer here would be “yes”, as an increase in block size would naturally equate to more compulsory misses (that would be more simply “misses” though rather than “miss rate”) but also just more data to process which won’t all necessarily fit into the fastest L1 cache. If we’re accessing a large amount of data with a large stride, we end up getting a higher non-compulsory miss rate as a result of more data being evicted from the cache before we utilize it, only to then redundantly load it back into a faster cache.
There is also a case where, if the block size is small enough and aligned properly, all the data will just fit into a single cache line and it wouldn’t matter so much how we sequentially access it.
Matrix Multiplication
Now here is a bit more complex case than the previous example above, but the same concepts tend to apply.
Let’s look at the first one:
1
2
3
4
5
6
7
8
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
accum = 0.0;
for (k = 0; k < n; k++)
accum += b[j][k] * a[k][i];
c[j][i] = accum;
}
}
If we look at the innermost k loop, we access b[j][k]. That’s a fairly optimal access pattern: “horizontal” if we imagine a row-order memory layout. However, we also access a[k][i]. That’s not so optimal, especially for a very large matrix, as it’s accessing memory in a vertical pattern with a large stride and will tend to suffer from data being evicted from the fastest but smallest forms of memory before it is used, only to load that chunk of data again redundantly.
If we look at the second j loop, that’s accessing c[j][i], again in a vertical fashion which is not so optimal.
Now let’s have a glance at the second example:
1
2
3
4
5
6
7
for (j = 0; j < n; j++) {
for (k = 0; k < n; k++) {
val = b[j][k];
for (i = 0; i < n; i++)
c[j][i] += val * a[k][i];
}
}
If we look at the second k loop in this case, it’s starting off accessing b[j][k] which is optimal (horizontal). Furthermore, it’s explicitly memoizing the value to val, which might improve the odds of the compiler moving that to a register and keeping it there for the following loop (this relates to compiler concepts related to aliasing, however, rather than CPU cache).
In the innermost i loop, we’re accessing c[j][i] which is also optimal (horizontal) along with a[k][i] which is also optimal (horizontal).
So this second version is likely to be more efficient in practice. Note that we can’t absolutely say that, as aggressive optimizing compilers can do all sorts of magical things like rearranging and unrolling loops for you. Yet short of that, we should be able to say the second one has higher odds of being more efficient.
“What’s a profiler?”
I just noticed this question in the comments. A profiler is a measuring tool that can give you a precise breakdown of where time is spent in your code, along with possibly further statistics like cache misses and branch mispredictions.
It’s not only good for optimizing real-world production code and helping you more effectively prioritize your efforts to places that really matter, but it can also accelerate the learning process of understanding why inefficiencies exist through the process of chasing one hotspot after another.
Loop Tiling/Blocking
It’s worth mentioning an advanced optimization technique which can be useful for large matrices – loop tiling/blocking. It’s beyond the scope of this subject but that one plays to temporal locality.