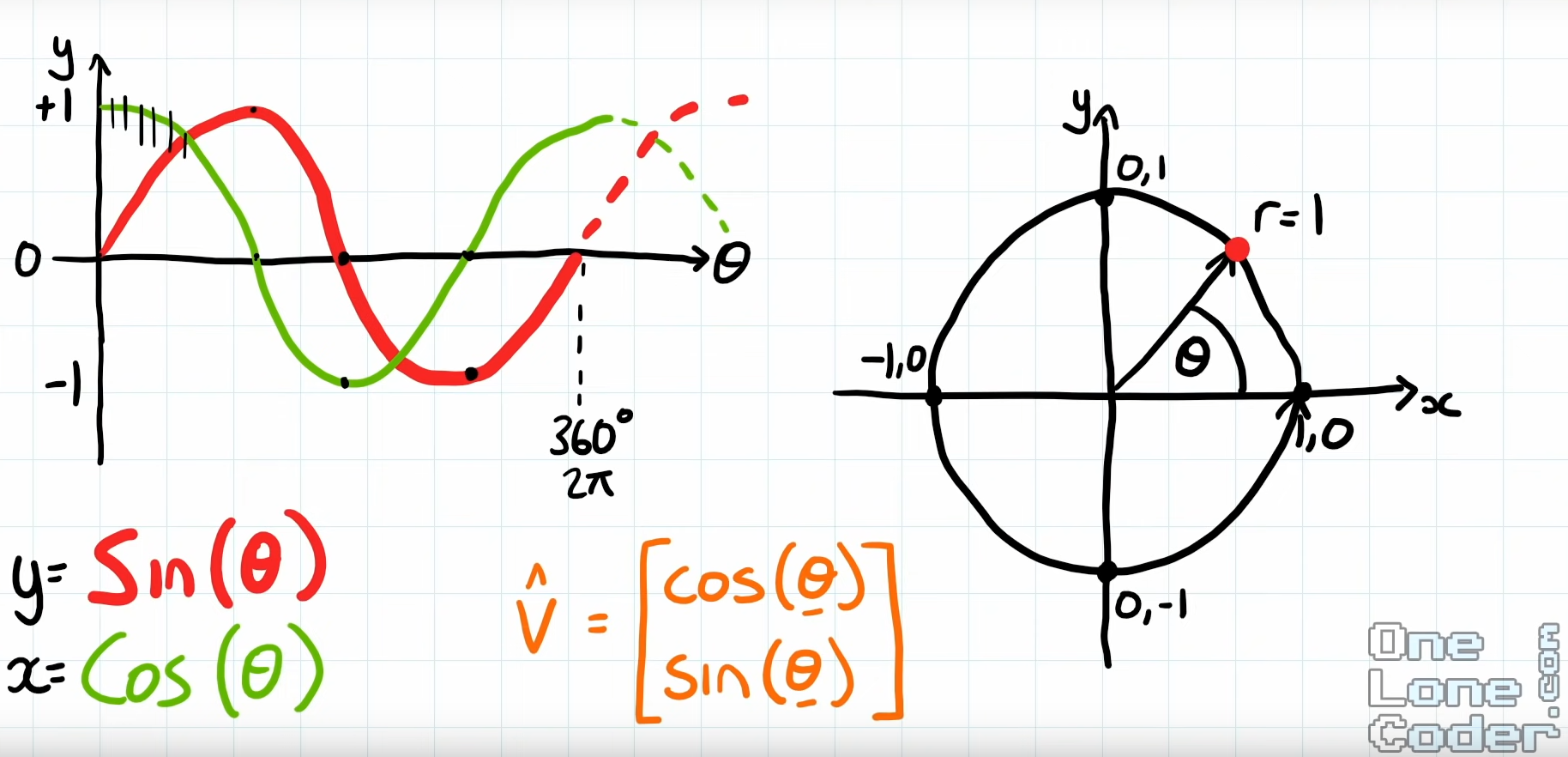GD - 1 Vectors and Math
Sebastian Lague, Essential math, Godot Vectors Complied by zenovak
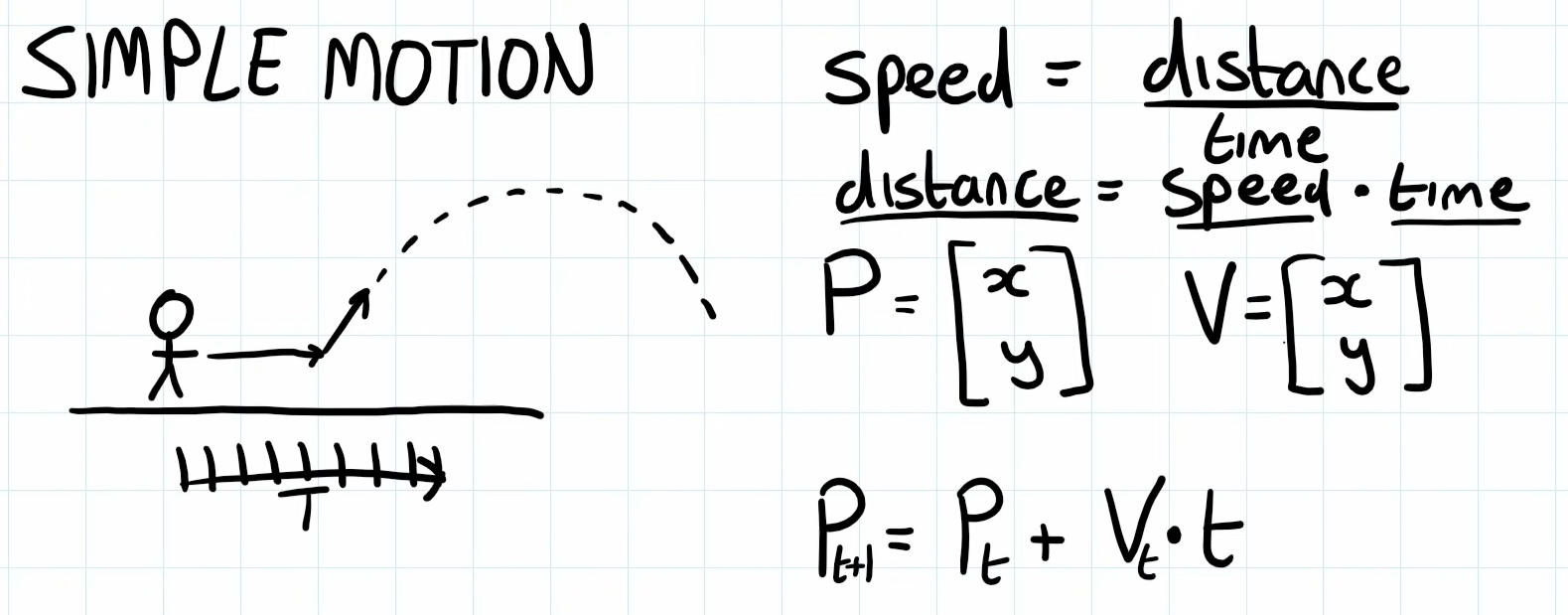
Understanding Vectors
In games, we often use Vectors to represent coordinates instead of Carstesians. These are not quite the same, although they are used interchangeably:
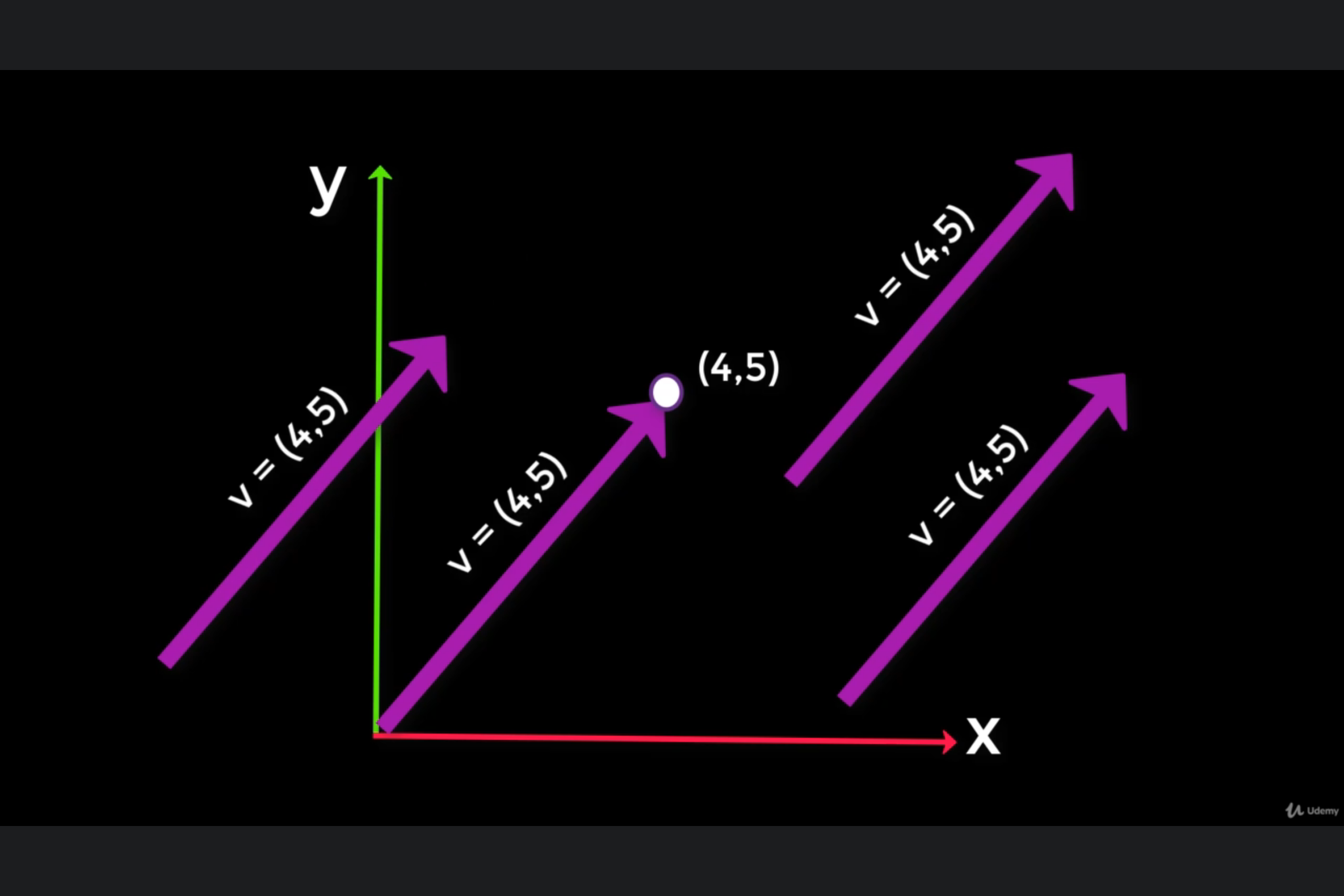
A vector is a value with magnitude(distance) and direction in space. It does not specify an origin. A (4. 5) vector can mean anything on a grid. It is a relative measurement, as depicted below.
When we work in 3D space, we use Vector3, and Vector2 in 2D space:
1
2
Vector3 = new Vector3(x, y, z);
Vector2 = new Vector2(x, y);
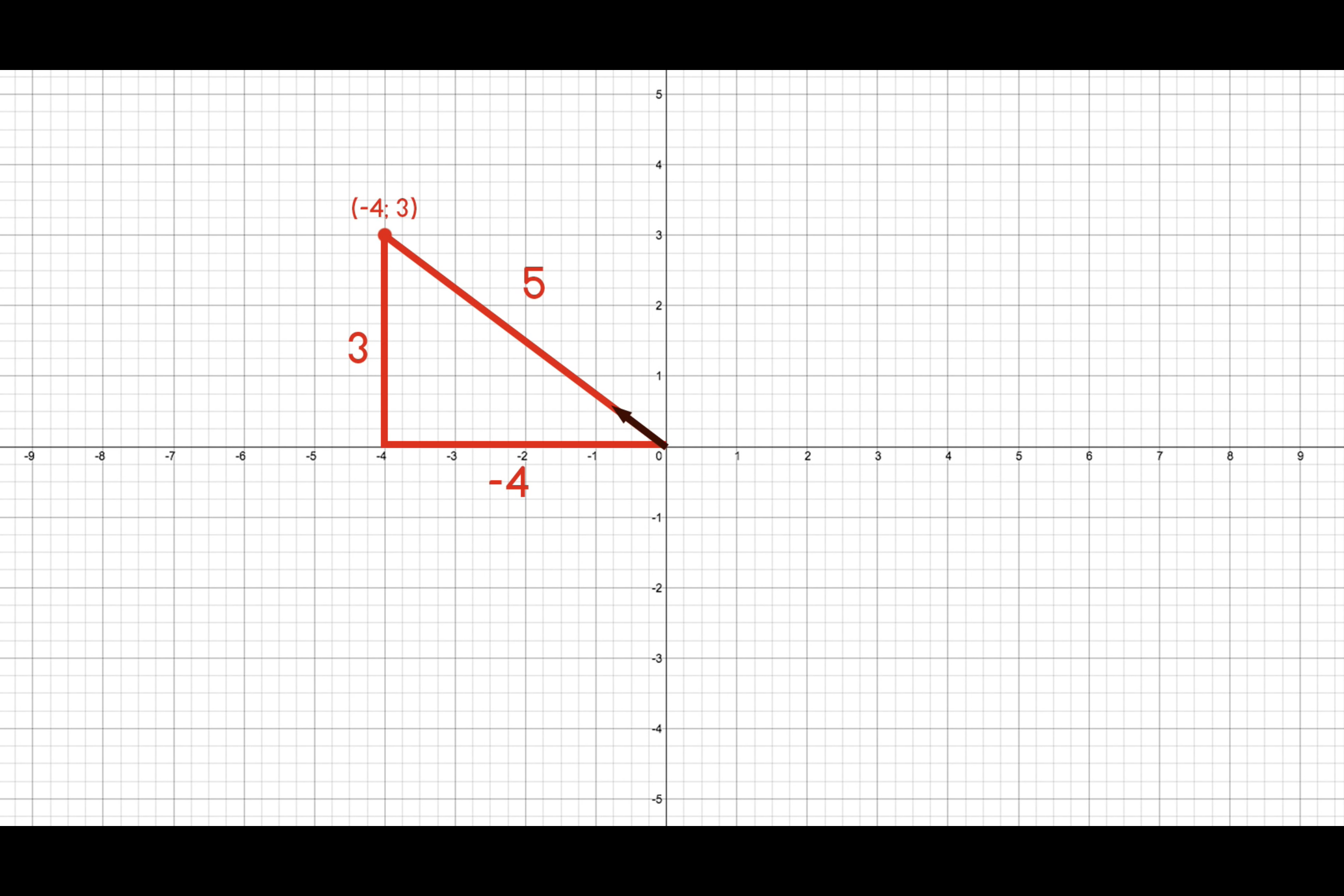
We can calculate the magnitude of the vector using pythogarams a^2 = b^2 + c^2 for length:
To calculate the directions, we divide the x and y value by the magnitude (-4, 3) / 5 = (-0.8, 0.6)
To get the magnitude of this directional vector, we get 1. SquareRoot((-0.8)^2 + (0.6)^2) = 1
Vector Normalisation
To demostrate this significance, imagine we have a player that presses down the W and A keys to strave up and left and so we use an input vector of (-1; 1). ^ba50cd
Say we want to move this player 3 units in that direction, we do: (-1; 1) * 3 = (-3; 3)
But if we now measure the magnitude: 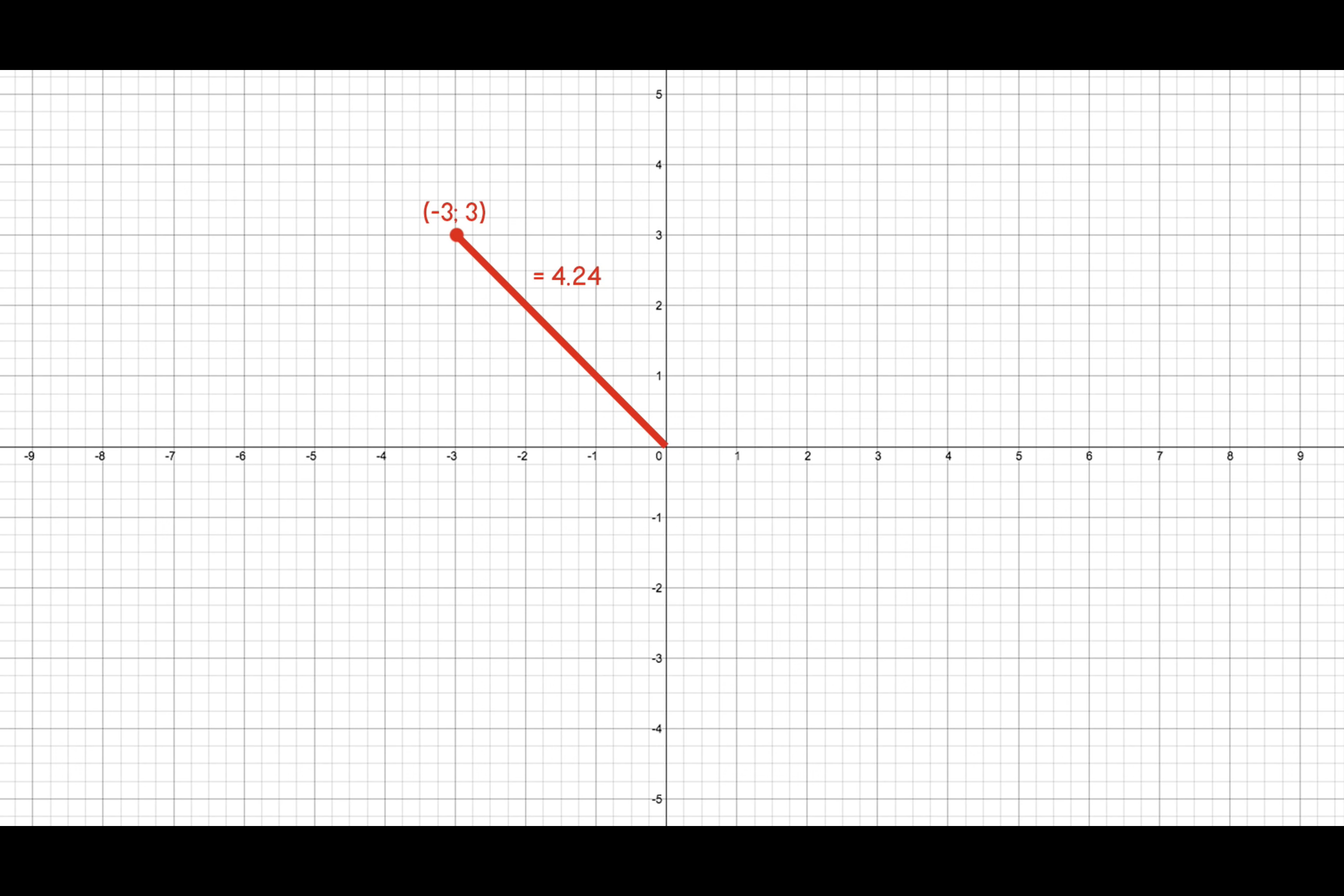 It is more than 3! The mistake we made has allowed player to move faster in the diagonal axis!!
It is more than 3! The mistake we made has allowed player to move faster in the diagonal axis!!
To correct this mistake, we must first normalize the vector. We can think of a normalized vector as the circle of directions for our vector. The input vector that we have used previously clearly lies outside the circle. 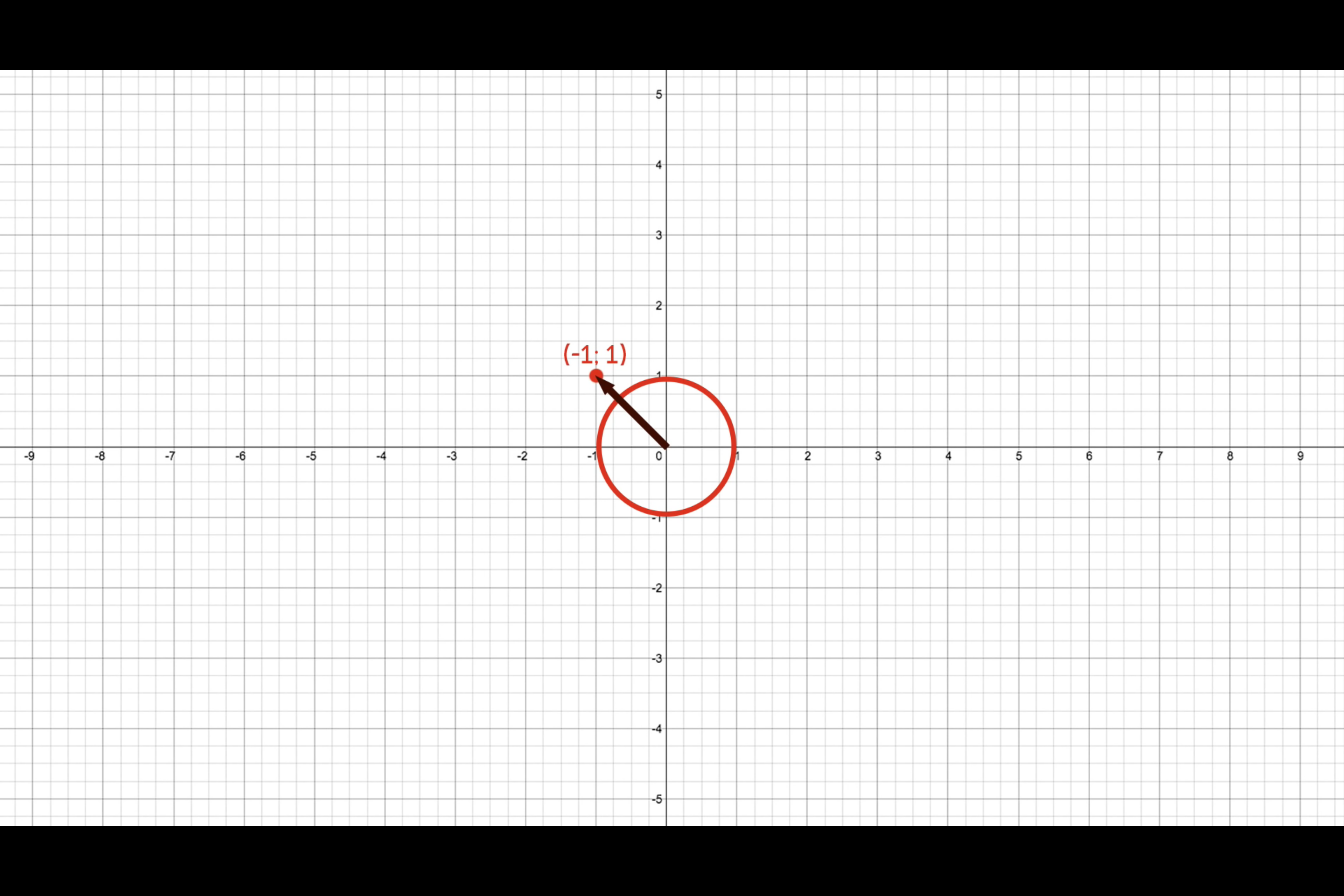
To normalize a vector we simple calculate its directions, which gives us (-0.71; 0.71) which lies inside the red circle. This is our normalized vector.
Move by 3 units: (-0.71; 0.71) * 3 = (-2.13; 2.13)
The new vector’s magnitude: 3.0122748878546926 Speed is preserved!
Practical use of vectors in games
Because vectors conveniently define X, Y (and Z value for Vector3). We use them to simply represents a point in space, like the cartesians. and thus the they are used interchangable.
However it is important to keep in mind of this mathematical fact that vectors simply represents magnitude and direction!
Subtract vectors == Direction & Distance offset
Let’s Imagine this, we have a vector to represent the current position of the player object, and another vector to represent an enemy object. 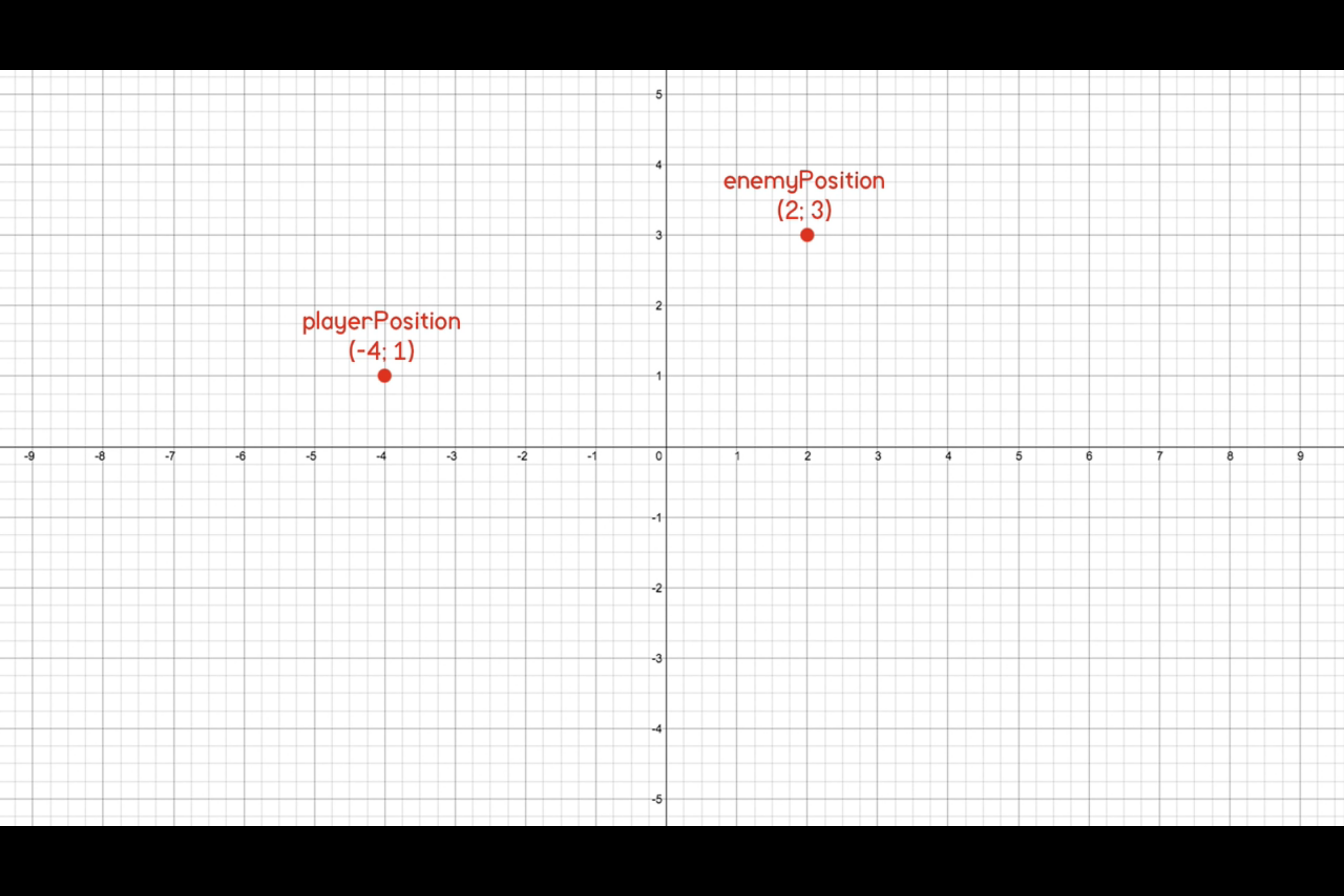
If we were to subtract the position of the player and the enemy we would get a (-6, -2) vector. 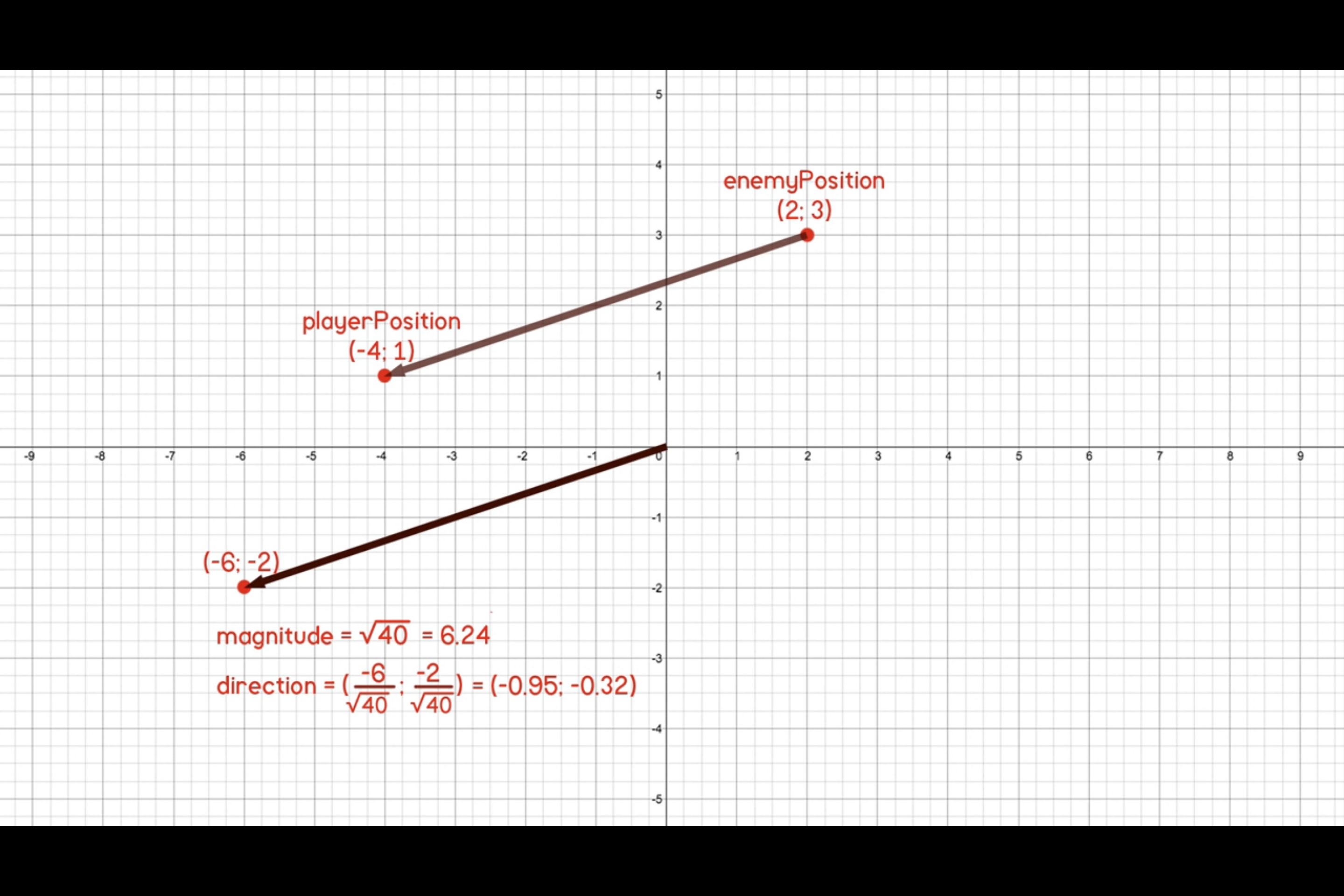 This Vector is insignificant if we think of it as a position on the grid. But as a vector it represents the displacement of the player from the enemy position. Its magnitude is the distance between the 2, and if we normalize it, we get the direction!
This Vector is insignificant if we think of it as a position on the grid. But as a vector it represents the displacement of the player from the enemy position. Its magnitude is the distance between the 2, and if we normalize it, we get the direction!
1
var directionToTarget = (targetPosition - myPosition).Normalized();
Add Vectors == new Force (Direction & Magnitude)
Let’s take 2 vectors. (0, 0) and (1, 0). Adding them together can represent a transformation of the vector.
This is used when we want to move a point around. Instead of positions. Often in this case vectors are treated as direction and magnitude of transformation. Often seen in calculating force and velocity
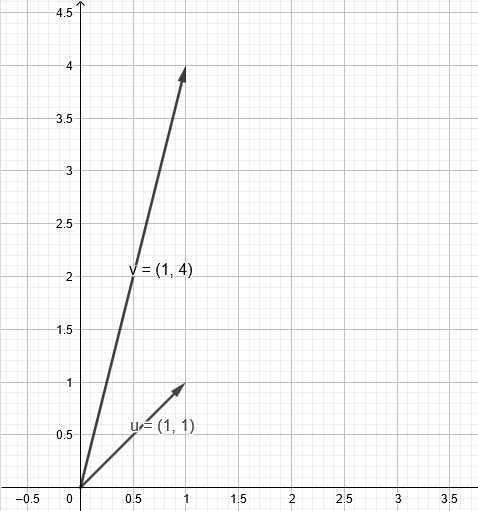
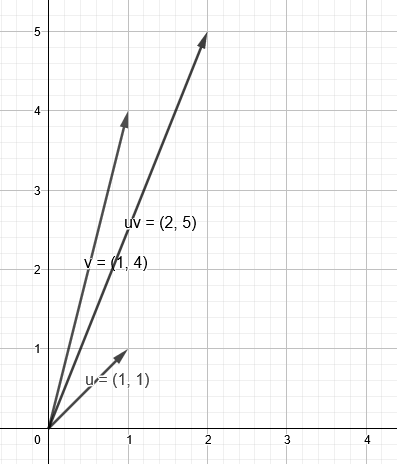
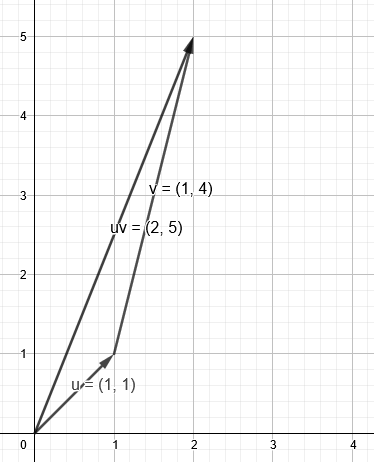
Let’s take these 2 Vector examples, and assume origin as being the object’s centre (Not game coordinate’s centre)
If we were to treat them not as coordinates, rather as a velocity, with u = (1, 1) being its initial velocity. Adding v = (1, 4) would make a new velocity.
It represents a new magnitude and direction its going.
Re-arranging the vectors, you can see what I mean,
Vector multiply by factor == add magnitude
We have seen this previously, multiplying a vector with a single number represents adding a scale of magnitude to an existing vector. This is especially useful for normalized vector.
Representation of Vectors in Unity
In unity Vectors are written as a struct:
1
2
3
4
5
6
7
8
public struct Vector3
{
public float x;
public float y;
public float z;
// Constructors and methods....
}
Reference: [[CS - 3 Non premitive types#Structs|About structs]]
In Unity Vectors come with useful methods so we dont have to write ourselves:
1
2
3
4
var myCarPos = new Vector3(3, 4, 5);
float speed = myCarPos.magnitude;
Vector3 direction = myCarPos.normalized;
Operators
1
2
3
4
5
6
7
8
9
10
11
// Vector * scalar:
(5, 10, 15) * 2 = (10, 20, 30)
// Vector / scalar:
(5, 10, 15) / 5 = (1, 2, 3)
// Vector + Vector:
(5, 10, 15) + (3, 4, 5) = (8, 14, 20)
// Vector - vector:
(5, 10, 15) - (3, 4, 5) = ( 2, 6, 10)
Common Computational pitfalls with Squareroots
When calculating the distance between two points in a Cartesian coordinate system (such as a graph), the traditional method involves using the square root of the sum of the squared differences in coordinates. This is known as the Euclidean distance formula, which you might have encountered in school.
However, Square root calculation typically uses the newtonian method of approximation and can be computationally expensive.
How is squareroot computed and why is it slow?
The newtonian method is an approximation of calculating a squareroot via iterations. You want to calculate the squaroot of a, and y is the squaroot, and x is a guessing estimate
1
2
3
y = x + a/x
--------
2
For example,
1
2
3
4
a = 4
x = 3
y = (3 + 4/3) / 2
y = 2.166666667
The results get closer to the correct answer if we repeat the formula with x being the new estimate, 2.1666667.
1
2
3
4
5
x = y
y = (2.166667 + 4/2.1666667) / 2
y = 2.00641
and repeat again
Effectively what we have is an algorithm like the following:
1
2
3
4
5
6
while (true) {
y = (x + a/x) / 2;
if y==x
break;
x = y;
}
However, floating point equality is never exact nor accurate so our endcase must be a comparision with epsilon instead. Where epsilon is the absolute smallest value of a float, or 0.00001, basically determines how close is close enough.
1
2
if abs(y-x) < epsilon:
break
Case 1 - Find the closest object
When we have many many many points that we need to calculate for e.g. physics simulations, or particle engine. Doing squareroots is not feasible, if we simply want to find the closest object. We must use a different method for calculating and comparing distances, called distance squared checks.
Distance squared checks
Instead of taking the square root, we compare the squared distances directly. In other words, you calculate the sum of the squared differences in coordinates but skip the final square root step.
The limitation of this is that, we are not returning the actual distances value, it is a truncated algorithm, but it speeds thing up massively for distance checking.
1
2
3
4
5
6
7
// Vector2 is float based.
float DistanceSquared(Vector2 a, Vector2 b){
var dx = a.x - b.x;
var dy = a.y - b.y;
return dx**2 + dy**2;
}
Case 2 - Normalized Vector (Unit Vector)
As we have seen previously to calculate a normalized vector, we need a distance component, Which is known to be computationally expensive.
1
var direction = (targetPosition - currentPosition) / distanceToTarget
However, calculating the unit vector doesn’t necessarily require a separate square root operation, as the magnitude can be computed and used within the normalization process without extracting its square root explicitly.
This is a common optimization technique when implementing vector normalization functions.
In many programming languages and libraries, vector normalization functions often take advantage of optimized routines and hardware instructions, making the process efficient even if a square root operation is involved. Additionally, some platforms provide intrinsics or functions that allow vectorized operations, further improving performance when dealing with multiple vectors simultaneously.
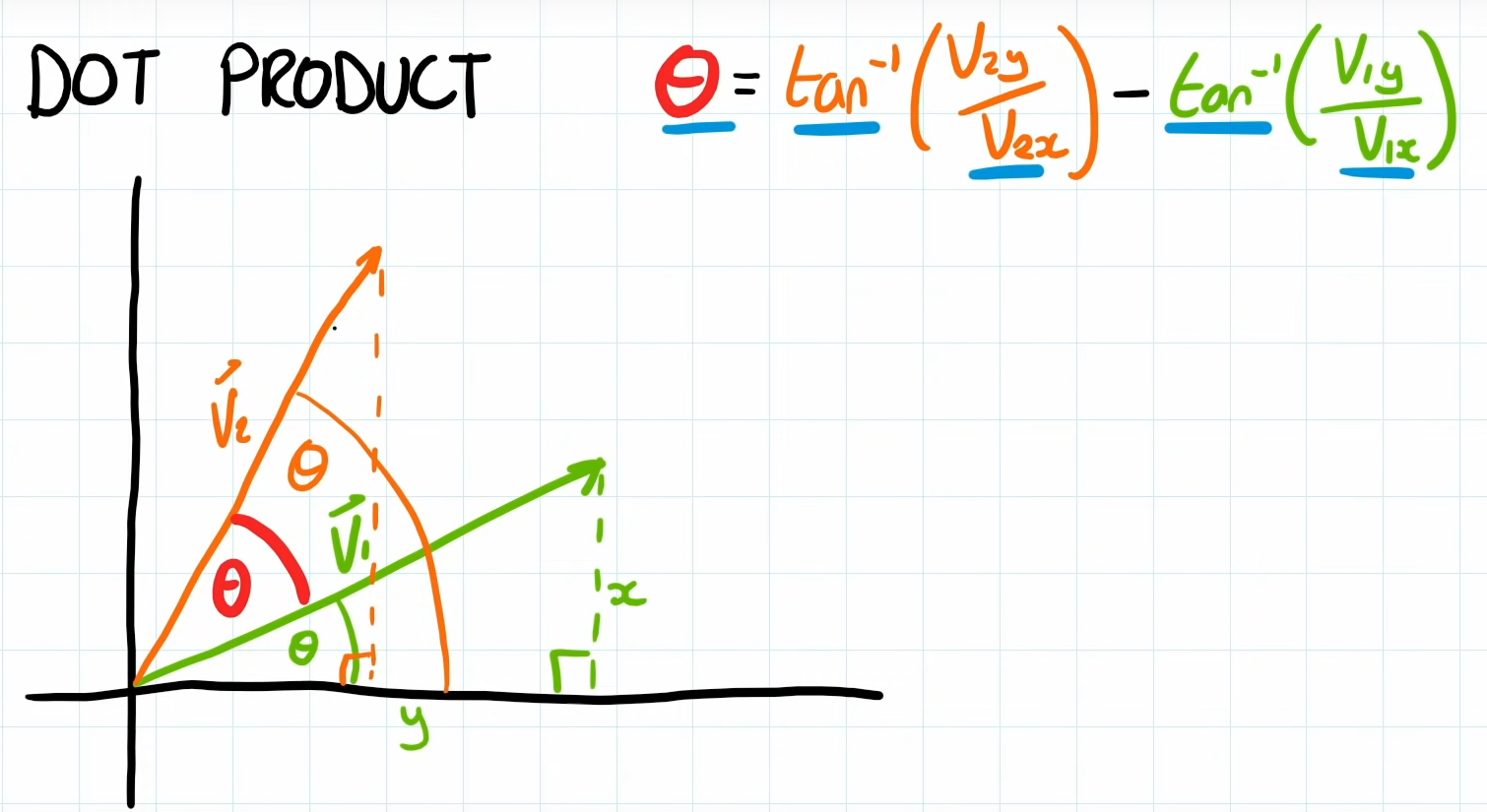
Vectors, Angles, and Rotations
Let’s assume another example a player and an enemy position. We know the direction of the enemy from the player via a normalized vector like [[G3 - Vectors and Math#^ba50cd|previously]]
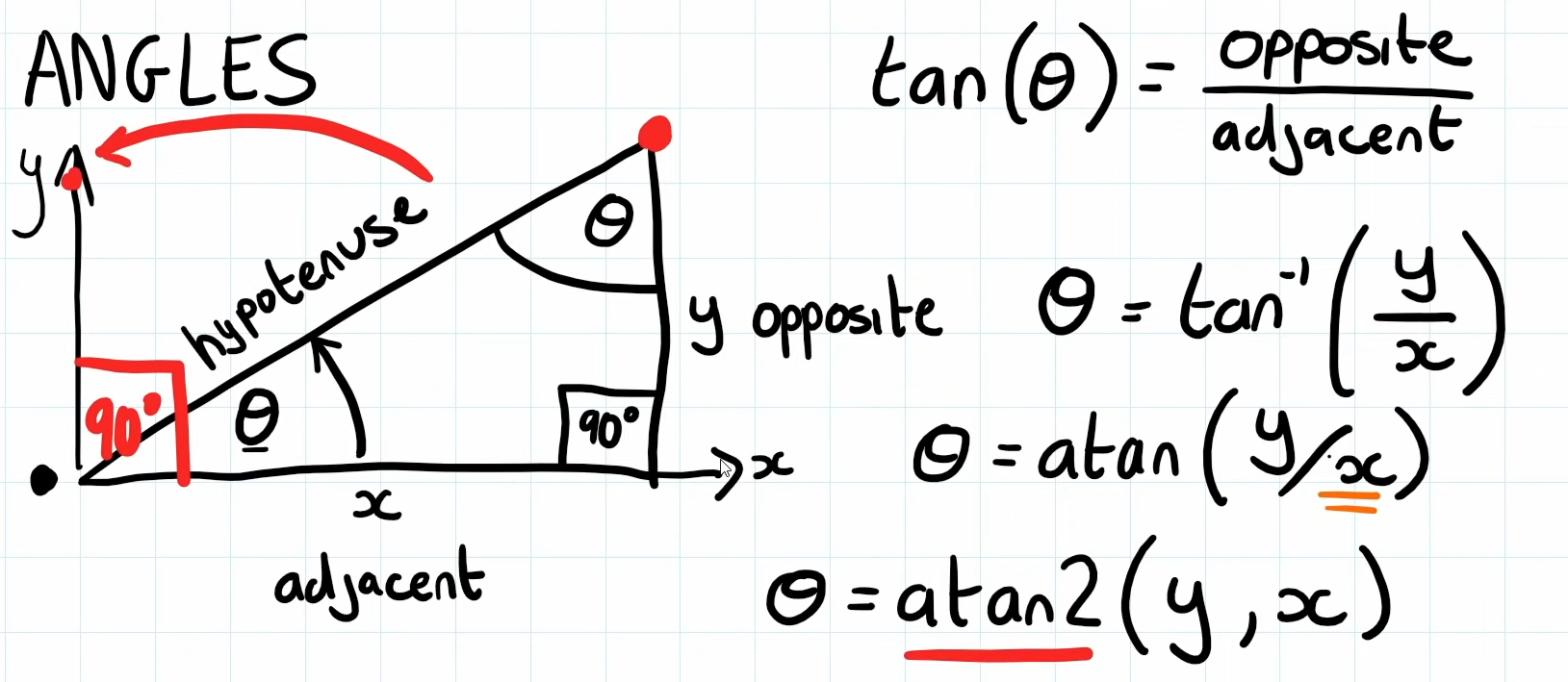
We calculate the angle via tangant:
Often in programming languages, tan^-1() functions are provided as atan(y, x) or atan2(y, x) with atan2() being safe for when x == 0;
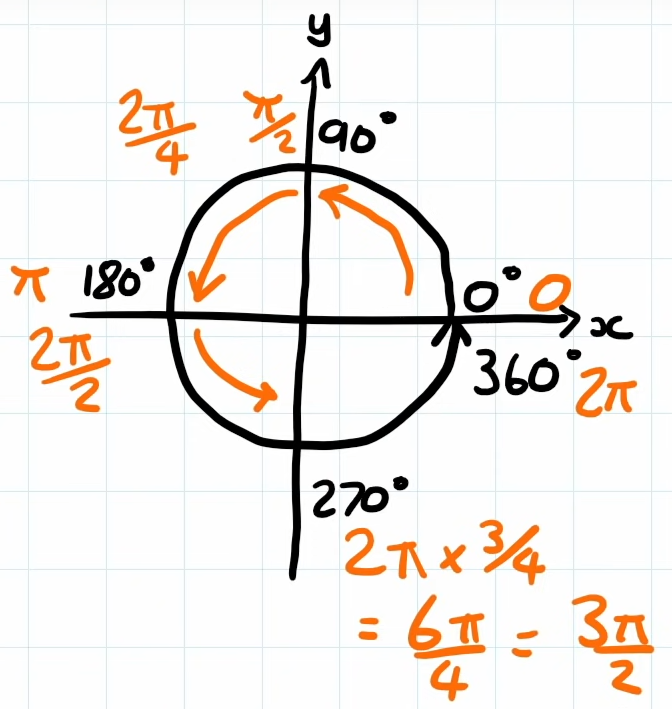
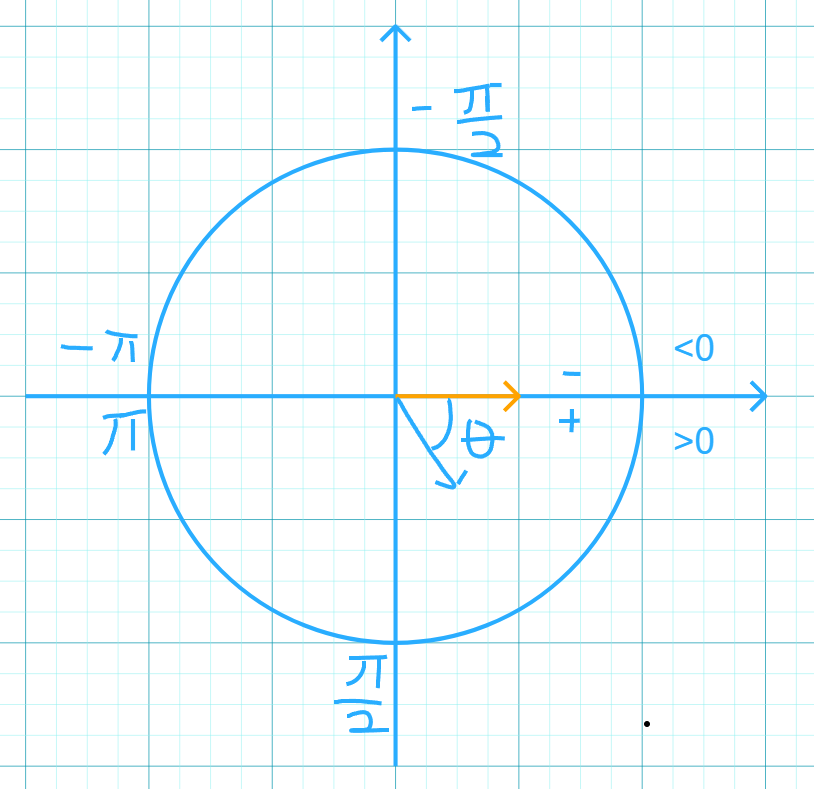
Radian representation of angles
In game engines, often angles are represented in Radian instead, which is a Pi float representation like:
1
radian = degrees / 180 * PI
Now, with a radian angle, we can just as easily get our normalized vector back via:
1
normalizedVector = (cos(angle), sin(angle))
How it represents rotation of game objects
In game engines, a rotation of our player character can just as easily be represented as a radian value of it, relative to the grid, or some other reference vector.
In godot
An object’s rotation is referenced with the X axis being the origin (1, 0), with pi represented as float. The equivalent of getting normalizedVector.Angle()
Computational pitfalls with trigonometry
Sin, Cos, tan are all computationally expensive math functions, just like squareroot, they require multiple CPU cycles to compute.
As we seen how vectors can be easily calculated. There are some common computational work arounds when dealing with radian maths using vectors instead.
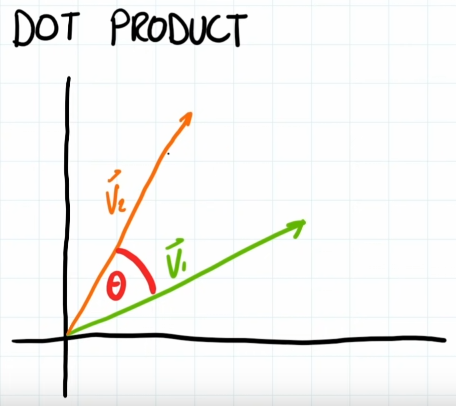
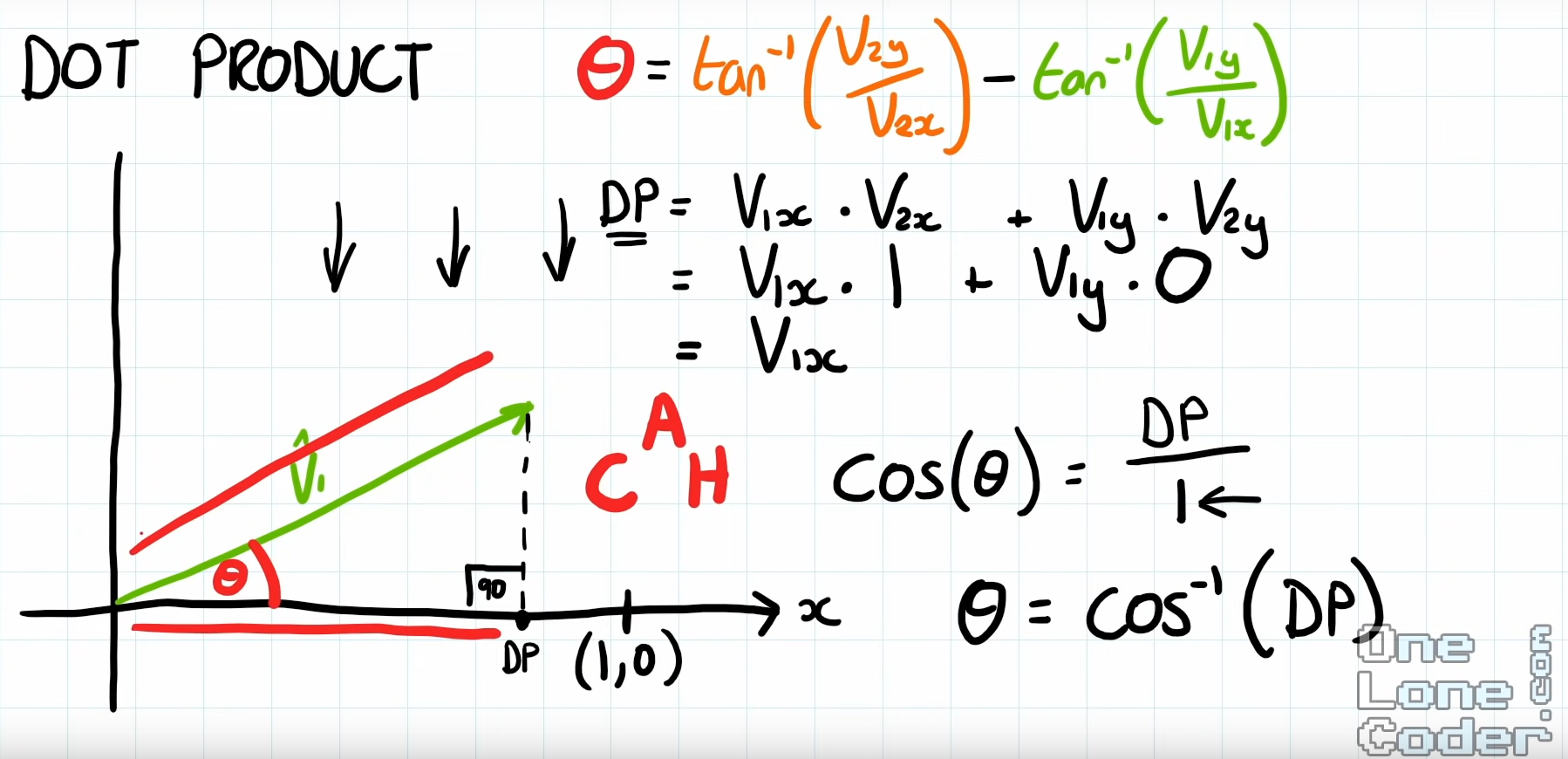
Vector dot product
Vector dot products allows us to think about angles in the domain of vectors. Let’s assume 2 normalized vectors v1, v2:
Traditionally we can calculate this via inverse tangan, which are computationally expensive.
Now, we know the angle between the 2 vectors wont change. We can simplify the calculations of the inverse tangent equation using dot products.
1
2
dotProduct = (V1x * V2x) + (V1y * V2y)
angle = inverseCos(dotProduct/ magnitude of V1)
Example, assume a vector (1, 1), we can calculate its angle with dot product via the following steps, Where the second vector is a constant X-axis projection.
1
2
3
var dp = dotProduct((1, 1), (1, 0));
var angle = inverseCos(dp / magnitudeOf((1, 1));
// magnitude not needed if vector is normalized
Rotating a Vector2
https://www.youtube.com/watch?v=MOYiVLEnhrw
Vector dot product usecases
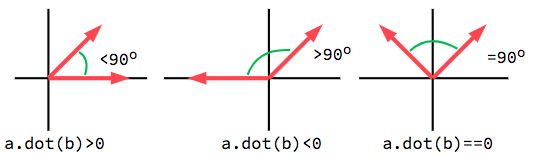
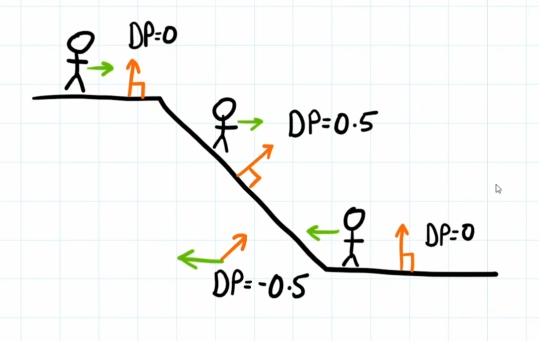
Direction similarity comparision with Normalized vectors
We use vector dot products on normalized vectors to identify their similarity in direction.
Let’s assume we have a constant vector direction, u being true to the x-axis, right side (1, 0). We test this with different normalized vectors, aiming at different axial directions,
Vector2.RightVector2.UpVector2.LeftVector2.Down
The dotproducts are as follows:
- 1
- 0
- -1
- 0
We can assume that facing a similiar direction will give a dotproduct closer to 1, while beyond 90 degrees, will go closer to -1. We can see this in action as:
dotProduct under unit vector
The demonstated dotProduct behavior only applies to unit vectors (Normalized Vectors).
In godot, Vector mathematics has convenient functions such as below to calculate a dot product of 2 vectors.
1
2
float c = a.Dot(b);
float d = b.Dot(a); // These are equivalent.
This is important when we compare the similarity of direction of vectors, when used for racing tracks etc.
isFacing?
We can also check for facing or look-at usecases:
1
2
if (Vector2.DotProduct(player.Rotation, player.DirectionTo(enemy)) < 0)
Console.WriteLine("You are facing away from enemy")
Where player.Rotation represents the player’s rotation on the global coordinate system in normalized vector format, and player.DirectionTo() being a shorthand function to calculate the normalized vector direction on the global coordinate system from the enemy
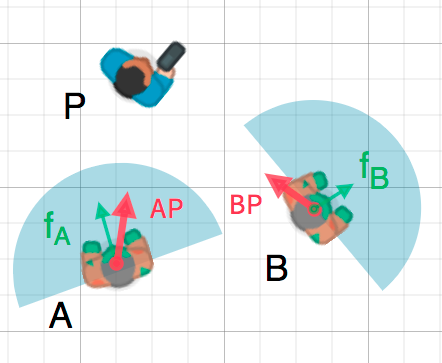
Let’s try another example. The green arrows fA and fB are unit vectors representing the zombie’s facing direction and the blue semicircle represents its field of view.
If the angle between this vector and the facing vector is less than 90°, then the zombie can see the player.
1
2
3
var AP = A.DirectionTo(P);
if (AP.Dot(fA) > 0)
GD.Print("A sees P!");
For zombie A, we find the direction vector AP pointing to the player using (P - A).normalized(), however, Godot has a helper method to do this called DirectionTo().
Vector Normals (Orthogonals)
A common use of unit vectors is to indicate normals. Normal vectors are unit vectors aligned perpendicularly to a surface, defining its direction. They are commonly used for lighting, collisions, and other operations involving surfaces.
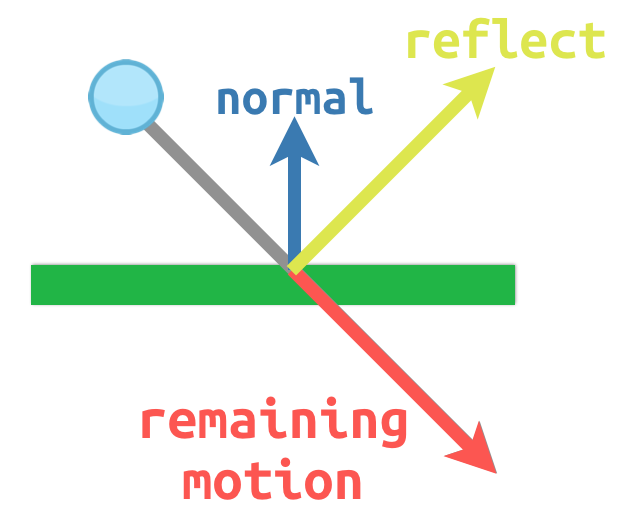 The surface normal has a value of
The surface normal has a value of (0, -1) because this is a horizontal surface.
Calculations for normals are computationally inexpensive as the formula to calculate the normals for a given vector is:
1
var normal = new Vector2(-vector.Y, vector.X);
The product would be a new vector pointing in the counter clockwise direction, 90 degrees.
In godot, a helper method exists vector.Orthogonal()
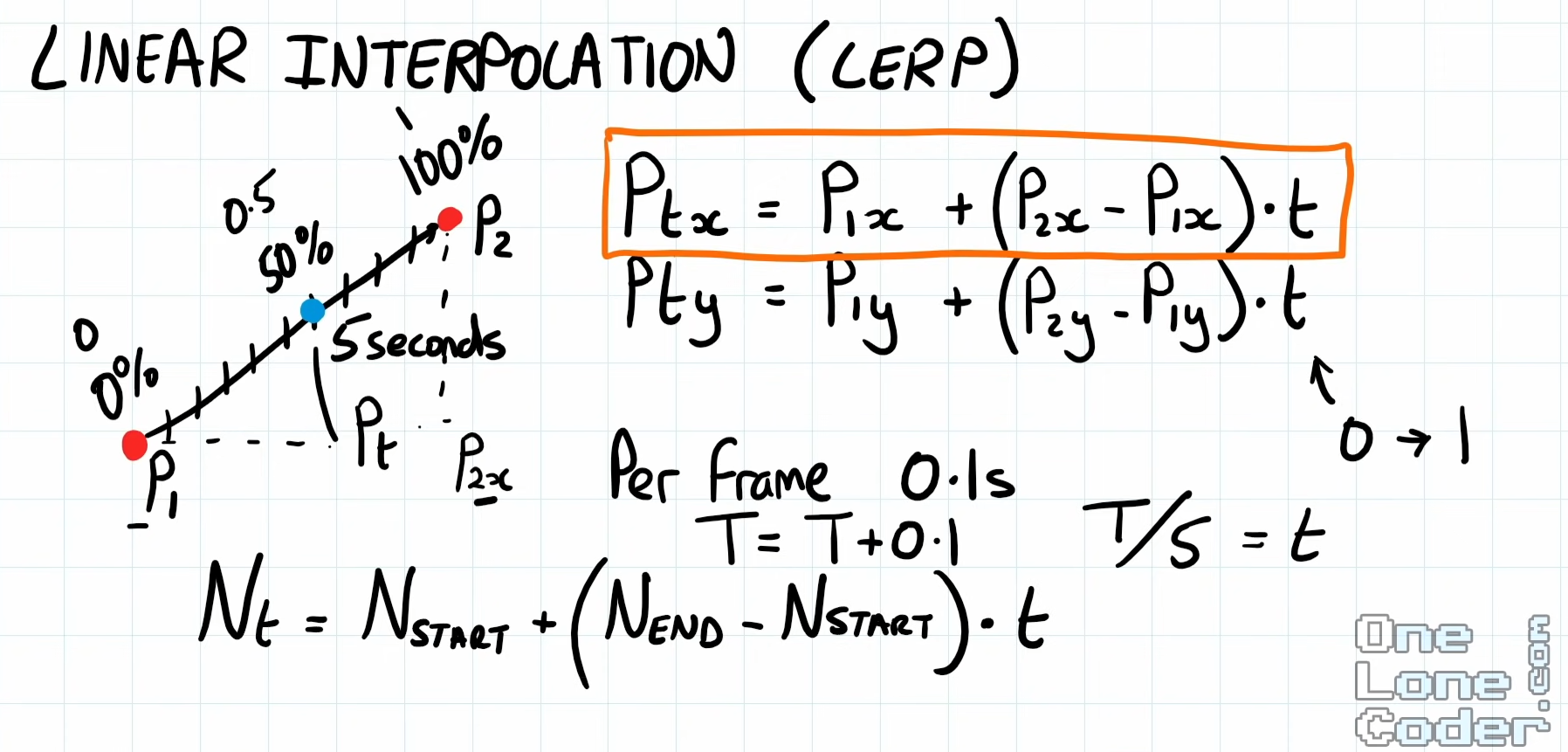
Linear interpolation (Lerp)
Linear interpolation is used for calculating steps to reach a vector location. Say we want to travel from P1 to P2, in 10 seconds.
What are the vector segments can we break this journey down for every second, and what is the vector for when we hit 5 seconds?
The equation is as simple as:
1
N(time) = NStart + (NEnd - NStart) * time
Usecase
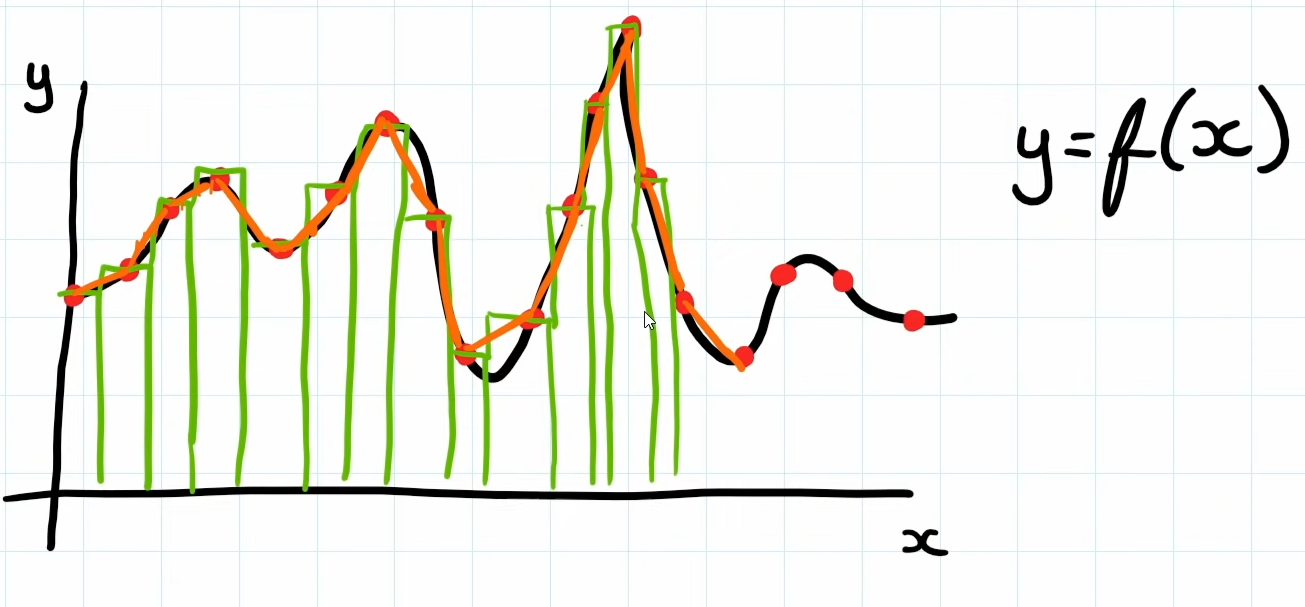
Linear interpolation is used for creating approximations to unknown functions, such as particle simulations, smoke etc. Given a noise graph, calculate what is the value at Point X, which sits between known point A and B.
Let’s say we want to stimulate a player’s movement path. Where Velocity is a vector2 and time is the time taken to render each physics frame, known as delta time
1
displacementTravelled = Velocity * time
We can see how we are now in familliar teritory.